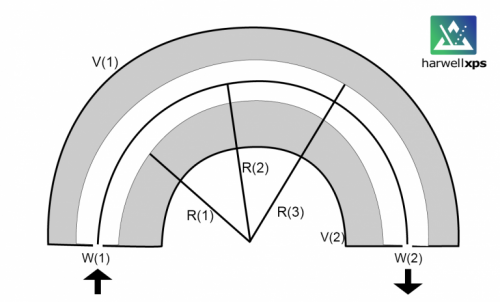
So here, we have 3 radii; R1 – the inner hemisphere, R2 – the centre of the hemisphere and R3 – the outer hemisphere. We also have a potential applied (V0) so that V1 on the outer hemisphere is negative and V2 is positive. Finally, we have slit widths – the entry slit, W1 and the exit slit, W2.
Note: R2 = (R1 + R3)/2
Electrons are retarded by the column and focused into the entry slit. The analyser is set to an energy, and any electrons which match this energy are refocused into the exit slit and detector, resulting in a signal. This energy is called the pass energy (EP). For example, if the pass energy is set to 20 eV, an electron travelling with a kinetic energy of 1000 eV would need to be slowed by 980 eV.
Energy is reduced as:
t = T – qVp
Where T = initial K.E., q = particle charge, Vp = decelerating voltage, t = resultant K.E.
For a given V0, only electrons of a specific EP may travel to the detector along R2.
Our resolution (ΔE) is dependant on pass energy (among other things) via the following relationship:
ΔE = EP . (W/2R2 + α2/2)
Where W is the slit width (W1 = W2) and α is the angle of acceptance.
Thus, for a higher pass energy, we observe poorer resolution (figure 2), though improved signal intensity.
